�������V�C�ɂȂ���!
�M�͊w�̑��@��
���M�͊w�̑��@��
���f�M���k
���f�M�c��
����M�ƔM�e��
����ϔ�M�ƒ舳��M����у}�C���[�̊W��
�����̓���
���C���X�x��
���C���X�x�͂Ɛ×͊w���t
���R���I���̗�
���n�t��
�����x��
���M�͊w�̑��@���i�G�l���M�[�Ǝd���j
�����̂����G�l���M�[�Ǝd���̊T�O
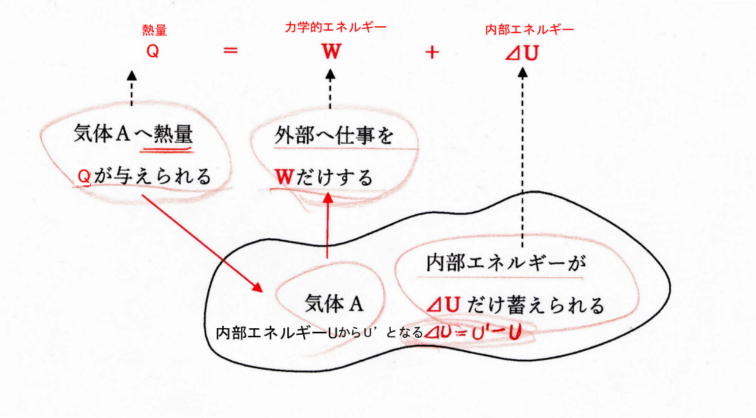
���̂��u���ꂽ��Ԃɂ��A���̕��̂������Ƃ��ł����u�G�l���M�[�v�������Ƃ��ł��܂��B���̂悤�ȁA���镨�̂����̕��̂������Ƃ��ł���G�l���M�[����������Ԃɂ��邱�Ƃ��u���̂��G�l���M�[�������Ă���v�Ƃ����܂��B�����āA���̕��̂����G�l���M�[�ɂ�葼�̕��̂ɗ͂������Ă��̗͂̕����։^�������邱�Ƃ��u�d���v�Ƃ����܂��B���̂悤�ɁA���̂̎����G�l���M�[�́A���̕��̂ɑ����d���iW�j��������͂�����܂��B
���ʒu�G�l���M�[�Ǝd��
�����ʒu�ɂ��镨��A���A���̐^���ɂ��镨��B�ɗ������ďՓ˂���ƁA���̏Ռ��ɂ�蕨��B�͓����܂��B����́A����A�������ɔ����G�l���M�[�������A���̃G�l���M�[�ɂ�蕨��B�������Ƃ����d�����������ƂɂȂ�܂��B���̂悤�ɁA�������Ƃ����ʒu�ɑ��݂�������A�������ƂƂȂ����G�l���M�[���u�ʒu�G�l���M�[�v�Ƃ����܂��B
���^���G�l���M�[�Ǝd��
�^�����Ă��镨��A������B�ɏՓ˂���ƁA���̏Ռ��ɂ�蕨��B�͓����܂��B����́A����A���^���ɔ����G�l���M�[�������A���̃G�l���M�[�ɂ�蕨��B�������Ƃ����d�����������ƂɂȂ�܂��B���̂悤�ɁA�^�����Ă��镨��A�������ƂƂȂ����G�l���M�[���u�^���G�l���M�[�v�Ƃ����܂��B
���͊w�I�G�l���M�[
��L���ʒu�G�l���M�[���^���G�l���M�[�����킹�����̂��A�u�͊w�I�G�l���M�[�v�Ƃ����܂��B
�͊w�I�G�l���M�[���ʒu�G�l���M�[�{�^���G�l���M�[
�������G�l���M�[
���̂ɂ́A�͊w�I�G�l���M�[�̑��ɁA�����G�l���M�[�iU�j�������������݂��܂��B�����G�l���M�[�Ƃ́A���̂̒��̊e���q�ǂ��������݂��Ɉ������肠�����q�Ԉ��͂ɂ��ʒu�G�l���M�[�ƁA���q�⌴�q�������M�^���ɂ��^���G�l���M�[�ł��B
�������A��C�ɂ��ẮA�e���q�Ԃ̋������傫���̂ŁA���̕��q�ǂ����̈��͂��قƂ�Ǔ����Ȃ����߁A���q�Ԉ��͂ɂ��ʒu�G�l���M�[�͖����ł��܂��B
���Q�l�F���q�Ȃǂ��������U�����Ă����ԁ��M���傫���@�@���q�Ȃǂ����܂�U�����Ă��Ȃ���ԁ��M��������
���M�͊w�̑��@��
���炩���������G�l���M�[�uU�v�������C�́uA�v�ɁA�M�uQ�v���^����ꂽ�Ƃ���ƁA����ɂ��C�́uA�v���̐ς̖c���ŊO���ɁuW�v�����d�������āA���x�㏸�ɂ������G�l���M�[���uU�f�v�ɂȂ����Ƃ���ƁA���̊W�͎��̂悤�ɂȂ�܂��B
U�{Q��W�{U�f�@�����ό`����ƁA�@Q��W�{�iU�f-U�j�@�ƂȂ�A�����ŁA�iU�f-U�j�͓����G�l���M�[�̕ω���\���Ă����A��U�̋L���ɒu�������邱�Ƃ��ł��܂��B
����ɂ�鎮���AQ��W�{��U�@�ƂȂ�A�M�͊w�̑��@���ƌĂ����̂ɂȂ�܂��B�B
���̎��́u�C�̂ɔMQ����������ƁAW�����d�������āA�����G�l���M�[����U��������v�Ƃ������Ƃ�\���Ă��܂��B
�܂�A�C�̂��M�G�l���M�[Q����������ƁA�ꕔ�͖c���Ƃ����d�������邽�߂̊O���ւ��͊w�I�G�l���M�[W�ƂȂ�A�c��͉��x�㏸�ɂ�葝���������x�������G�l���M�[��U�Ƃ��Ē~������Ƃ������ƂɂȂ�܂��B���̓����G�l���M�[�́A�_�̂ł��郁�J�j�Y�����l�����ŏd�v�ȊT�O�ƂȂ�܂��B
�܂�A�M�͊w�̑��@���Ƃ́A�u�M�v�Ɓu�d���v�͓������̂ł���A�u�M����d���ցv�A�u�d������M�ցv�ϊ����邱�Ƃ��ł��A���̊Ԃɂ����Ă̓G�l���M�[���ۑ������Ƃ������Ƃ��`�������̂ł��B
��TOP
���f�M���k
�r�ɓ������C��A���s�X�g���ʼn����ē����̋�C�����k���܂��B���̎��A�u�C��A�̓s�X�g���ɂ��d�������ꂽ�v���ƂɂȂ�܂��B�s�X�g�����炳�ꂽ�d��W�̕����������G�l���M�[���������܂��B�����G�l���M�[����������ƁA�M�������Ă��Ȃ��̂ɋC��A�̉��x���㏸���܂��B������f�M���k�ɂ��f�M�����ƌ����܂��B
��قǂ̔M�͊w�̑��@���̎��ł́AQ�i�C��A�։�����ꂽ�M�ʁj��W�i�O���ɂ����d���j�{��U�i�~����ꂽ�����G�l���M�[�j�ł������A���̒f�M���k�ł͊O�������������u�M��Q�v�͂Ȃ��̂ŁA�O�����炳�ꂽ�u�d��W�v�̃G�l���M�[�̕����������G�l���M�[���������邱�ƂɂȂ�܂��B���������Ēf�M���k�ł͎��̎������藧���܂��B��U�i�����G�l���M�[�j���f�M���k�O�̓����G�l���M�[�{W�i�O�����炳�ꂽ�d���j
���f�M�c��
�r�ɋC��A����������ԂŃs�X�g���������܂��B���̎��s�X�g���͋C��A�ɉ����グ��ꂽ�悤�ɂ������܂��B�Ȃ̂ŁA������u�C��A���s�X�g���Ɏd���������v�Ƃ����A�d�����������A�����G�l���M�[������āA�C��A�̉��x��������܂��B������A�f�M�c���ɂ��f�M��p�Ƃ����܂��B
�����ł́A���̎������藧���܂��B��U�i�����G�l���M�[�j���f�M�c���O�̓����G�l���M�[�|W�i�O���ւ����d���j
����M�Ƃ́A���͂܂��͑̐ψ��̏������ŁA�����Pg�i�Ώە��͈�̓_�j�̉��x���PK�i�P���r���j�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B��M�e���Ƃ������܂��B�������ώ��ł���Ε����̎��ʂɔ�Ⴗ�邽�߁A��M�͒P�ʎ��ʓ�����ƒ�߂��Ă��܂��B�P�ʂ��i/���E�j�i�W��-���p�[�O�����P���r���j�ŁA��M�̋L����c�i�X���[��c�j�ł��B
��M�̐��l�́A���ꂼ��̕����ɂ���ĈقȂ�܂��B�Ⴆ�A��M�������������͏��Ȃ��M�ʂʼn��x���ω����邽�߁A���܂�₷���A��߂₷�������������Ă��܂��B�t�ɁA��M���傫�������́A���x���グ�邽�߂ɑ����̔M�ʂ�K�v�Ƃ��A���܂�ɂ����A��߂ɂ��������������Ă��܂��B
��ȕ����Pg������̔�Mc�i�Q�l�l�j�@�P�ʂ͂i/���E�j
���u���v��u��C�v�̂悤�ɁA�����������ł����̕����̏�Ԃ≷�x���ς��Ɣ�M���ς��܂��B
���M�e���Ƃ��A���͂܂��͑̐ψ��̏������ŁA�����i�Ώە��͓_�i�����j�̏W���́j�̉��x���PK�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B��M�ɕ��̂̎��ʂ��|�������̂ŁA�P�ʂ��i/�j�i�W��-���p�[�P���r���j�ŁA�M�e�ʂ̋L�����b�i���[�W�b�j�ł��B
���ɂ���Ɓ@C�������@�@�iC�F�M�e��J/K�@�@���F���ʂ��@�@���F��M�i/���E�j�j
����ϔ�M�Ƃ́A�̐ρivolume�j���̏������ŁA�P�ʗʂP�s������̕����̉��x���PK�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B��e��M�Ƃ������܂��B�P�ʂ͂i/�j���E�j�i�W��-���p�[�L���O�����P���r���j�ŁA�L����Cv�ł��B
���舳��M�Ƃ́A���́ipressure�j���̏������ŁA�P�ʗʂP�s������̕����̉��x���PK�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B�P�ʂ͂i/�j���E�j�i�W��-���p�[�L���O�����P���r���j�ŁA�L����Cp�ł��B
���}�C���[�̊W��
�舳��MCp�|��ϔ�MCv��R�i�C�̒萔�j
���z�C�̂ɂ����āA�舳��MCp�ƒ�ϔ�MCv�̍��͋C�̒萔R�ɓ������B
�P�@�ő̂̕X�́A�t�̂̐����̐ς��傫���y���B
�Q�@���̉t�̂ɔ�ׂāA�Z�_�ƕ��_�������B
�R�@���q���m�����т���͂������̂ŁA�\�ʒ��͂��傫���B
�S�@��M���傫���̂ŁA�R�ĕ����̍��M���ɐ����|����ƁA�������㏸���ĕ�������܂łɂ��̔R�ĕ��������R�̔M��D���B�B
�T�@�����M�i�C���M�j���傫���̂ŁA�����C�́i�����C�j�ɂȂ�Ƃ��Ɏ��͂��瑽���̔M��D���B
�U�@�M�`�����������B
�V�@�l�X�ȕ�����n�����B
��TOP
�C���̍�����C��́A�C���̒Ⴂ��C��̕��ֈړ����悤�Ƃ��܂��B���̗͂��C���X�x�͂Ƃ����܂��B�C���̍����傫���قǁA���̋C���X�x�͂͑傫���Ȃ�A��C�Ɉړ���������͂ƂȂ��ĕ��������܂��B
��TOP
��TOP
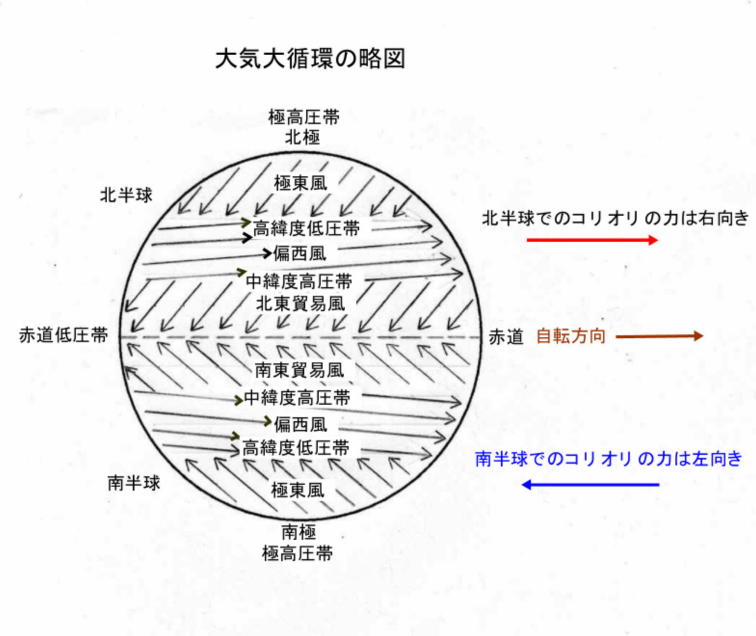
�R���I���̗͂Ƃ́A�n���̎��]�ɂ���ē����͂ł��B�]�����Ƃ������܂��B
�n���̎��]�́A�k�ɓ_�ォ�猩��Ɣ����v���A��ɓ_�ォ�猩��Ǝ��v���ɉ�]���Ă��܂��B
���������āA�k�����ɂ����āA�k�シ�镨�̂͏��X�ɓ����ɐi�ނ悤�Ɍ����A�쉺���镨�̂͏��X�ɐ����ɐi�ނ悤�Ɍ����܂��B���́u�������̗́v���R���I���̗͂Ƃ����܂��B
�R���I���̗͂́A������ς���͂͂���܂����A������ς���͂͂���܂���B
���ɁA�R���I���̗͂̑傫���ɂ��čl���܂��B
�R���I���̗͂́A�ԓ��ł͂O�i�[���j�ł����A���ܓx�قǑ傫���Ȃ�A�k�ɂƓ�ɂł͍ő�ƂȂ�܂��B
����ɁA�R���I���̗͂��傫���Ȃ�v�f�Ƃ��ẮA���ܓx�̂ق��A���ʂ��傫���A���̂̑��x�������A�قǑ傫���Ȃ�܂��B
�R���I���̗͂̑傫�������ɂ���Ǝ��̂悤�ɂȂ�܂��B
���R���I���̗́�
F�����~�Q��Vsin���i�Q�I���K�@���C�@�T�C���@�t�@�C�j�@
�e�F�R���I���̗́@�@
���F���ʁi�����j�@�@
���F�n���̊p���x�i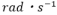 �j�܂��́i
�j�܂��́i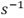 �j�Łirad�̓��W�A���j�@�p���x�Ƃ͂P�b�Ԃ̉�]����\�������l�@
�j�Łirad�̓��W�A���j�@�p���x�Ƃ͂P�b�Ԃ̉�]����\�������l�@
V�F���̂̑��x�i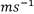 )�@�@
)�@�@
���F�ܓx
���R���I���p�����[�^��
��L�@�̎��̂����A����m�ƕ��̂̑��xV�ȊO�̐��l�͈ܓx�ɂ���Č��܂���̂Ȃ̂ŁA����m�ƕ��̂̑��xV���u�P�v�Ƃ��Ď��̎��ɂȂ�܂��B������A�R���I���p�����[�^�Ƃ����܂��B
�����Q��sin���@�i�R���I�����q�܂��͘f���ߓx�Ƃ������܂��j�A
���F�n���̊p���x
���F�R���I���������ꏊ�̈ܓx
���@�̎��̂����A���ʂƕ��̂̑��x�ȊO�̒l�͈ܓx�ɂ���Č��܂�̂ŁA���̎����R���I���p�����[�^�Ƃ���B
���@�̎����A�̎���������Ɓ�
F=mVf�@�B�@
���̎����C�ی��ۂɓ��Ă͂߂��ꍇ�̊e�v�f��
m�F��C��̎���
V�F����
���F���]�̊p���x�̒l�i�V�D�Q�X�Q�~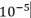
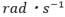 �j
�j
���F�R���I���p�����[�^
�ƂȂ�܂��B
���@���B�̎��̎��ʂ����P�����Ƃ����P�ʎ��ʂ�p����ƁA�@���B�̎��͂��ꂼ�ꎟ�̂悤�ɂȂ�܂���
F���Q��Vsin���@�@�f
F=Vf�@�B�f
���ꂪ�A�P�ʎ��ʂP�s�̋�C��ɓ����R���I���̗͂̑傫���ɂȂ�܂��B�P�ʂ�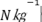 �iN�̓j���[�g���j�ł��B
�iN�̓j���[�g���j�ł��B
�����ŁAF=mVf��F�����~�Q��Vsin���̎�����A�R���I���̗�F�Ǝ��ʂ��E�R���I���̗�F�ƕ��̂̑��x�u�E�R���I���̗�F�ƃR���I���p�����[�^���E�R���I���̗�F��sin���i�R���I���p�����[�^�ɂ��Q���̒l�i�V�D�Q�X�Q�~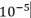
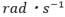 �j�͈��Ȃ̂ŁB�j�́A���ꂼ����W�ɂ��邽�߁A���̊W�����藧���܂��B
�j�͈��Ȃ̂ŁB�j�́A���ꂼ����W�ɂ��邽�߁A���̊W�����藧���܂��B
���������̏ꍇ�̃R���I���̗͈͂ܓx�Ō��܂�B
�ܓx�����̏ꍇ�̃R���I���̗͕͂����Ō��܂�B
�ƂȂ�܂��B
�Q�l�܂ŁA�ܓx���Ƃ̃R���I���̗͂̑傫�����v�Z���Ă݂܂��B
F���Q��Vsin���@���̎������Ɉܓx�̐��l�Ă͂߂܂��B
���ܓx�����k�܂O�x�i�ԓ���j
F���Q��Vsin�O���@sin0�����O
F���Q��V�~�O�@
F���O�i�[���j
�ԓ���ł̓R���I���̗͓͂����Ȃ��B
���ܓx�����k�܂R�O�x
F���Q��Vsin�R�O���@sin�R�O�����O�D�T
F���Q��V�~�P�@
F����V
���ܓx�����k�܂X�O�x�i�k�Ɂj
F���Q��Vsin�X�O���@sin�X�O�����P
F���Q��V�~�P�@
F���Q��V
�k�ɂƓ�ɂł̓R���I���̗͍͂ő�ƂȂ�B
��TOP
�Î~���Ă����C��ɂ͋C���X�x�͂��͂��炢�āA���C���������C�����Ɍ������ĕ��ƂȂ��ē����n�߂܂��B
���̑��xV�����������ƁA���̕����ɔ�Ⴕ�ăR���I���������傫���Ȃ�܂��iF���Q��Vsin���j�B�k�����Ŗk�シ�镗�́A�R���I���̗͂��傫���Ȃ�قǂɁA�E���i�����j�ւƋȂ�����悤�ɂȂ�܂��B�ŏI�I�ɂ́A�C���X�x�͂ƃR���I���̗͂��o�����X��ۂ��āA�������ɉ����ĕ��������悤�ɂȂ�܂��B���ꂪ�n�t���ł��B�n�t���ɂȂ�ƁA�����͂���ȏ��������邱�Ƃ��Ȃ��A�܂��������ς��Ȃ����肵�����ƂȂ�܂��B
�k�����Ŕ�������n�t���́A��C�����i�ፂ�x���j������Ɍ���悤�ɂ��Đ����܂��B�씼���ł͋t�ɁA��C�������E��Ɍ���悤�ɂ��Đ����܂��B
�Ȃ��A�C���X�x�͂ƃR���I���̗͂��ނ荇������Ԃ��n�t�����t�Ƃ����܂��B
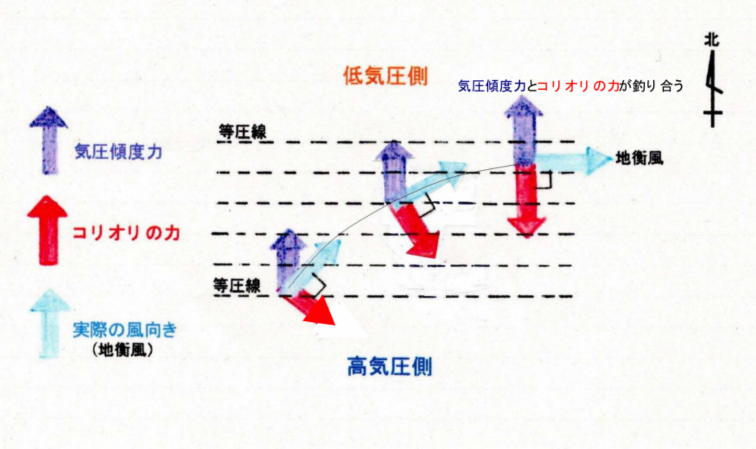
���n�t���̕��������߂�
�n�t���́A�C���X�x�͂ƃR���I���̗͂��o�����X�i�C���X�x�́��R���I���̗́j���Ƃ��Ă���̂ŁA���̎��ɂ��n�t���̕��������߂邱�Ƃ��ł��܂��B

��TOP
���x���͎��ۂɐ����Ă��镗�ł͂Ȃ��A�Q�n�_�̕��x�N�g���̍��������܂��B
�n���̑�C�́A�ԓ��t�߂ł͒g�����A�k�ɕt�߂ł͗₽���B
�ԓ����̒g������C��͖c������̂ŁA���̓����ʂ́A���x�̍������Ɉʒu����B
�t�ɁA�k�ɑ��̗₽����C��͈��k����̂ŁA���̓����ʂ́A���x�̒Ⴂ���Ɉʒu����B
���������āA���̒g�C�Ɗ��C�̊Ԃɂ��C���X�x���������āA�n�t������������B
�C���X�x�͂͏��قǑ傫���Ȃ邽�߁A�n�t�������قǑ傫���Ȃ�A�n��ɋ߂��قǒn�t���͏������Ȃ�B
���̎��̕����̍��i�Q�n�_�̕��x�N�g���̍��j�����x���Ƃ����B
�k�����ł̒n�t���́A�E����g������C�i�ԓ����j�A������₽����C�i�k�ɑ��j�Ƃ��鐼���ƂȂ��Ă��邽�߁A���x�����g������C���E���ɂ��Đ����ƂȂ��Ă���B

��TOP
���f�M���k
���f�M�c��
����M�ƔM�e��
����ϔ�M�ƒ舳��M����у}�C���[�̊W��
�����̓���
���C���X�x��
���C���X�x�͂Ɛ×͊w���t
���R���I���̗�
���n�t��
�����x��
���M�͊w�̑��@���i�G�l���M�[�Ǝd���j
�����̂����G�l���M�[�Ǝd���̊T�O
���̂��u���ꂽ��Ԃɂ��A���̕��̂������Ƃ��ł����u�G�l���M�[�v�������Ƃ��ł��܂��B���̂悤�ȁA���镨�̂����̕��̂������Ƃ��ł���G�l���M�[����������Ԃɂ��邱�Ƃ��u���̂��G�l���M�[�������Ă���v�Ƃ����܂��B�����āA���̕��̂����G�l���M�[�ɂ�葼�̕��̂ɗ͂������Ă��̗͂̕����։^�������邱�Ƃ��u�d���v�Ƃ����܂��B���̂悤�ɁA���̂̎����G�l���M�[�́A���̕��̂ɑ����d���iW�j��������͂�����܂��B
���ʒu�G�l���M�[�Ǝd��
�����ʒu�ɂ��镨��A���A���̐^���ɂ��镨��B�ɗ������ďՓ˂���ƁA���̏Ռ��ɂ�蕨��B�͓����܂��B����́A����A�������ɔ����G�l���M�[�������A���̃G�l���M�[�ɂ�蕨��B�������Ƃ����d�����������ƂɂȂ�܂��B���̂悤�ɁA�������Ƃ����ʒu�ɑ��݂�������A�������ƂƂȂ����G�l���M�[���u�ʒu�G�l���M�[�v�Ƃ����܂��B
���^���G�l���M�[�Ǝd��
�^�����Ă��镨��A������B�ɏՓ˂���ƁA���̏Ռ��ɂ�蕨��B�͓����܂��B����́A����A���^���ɔ����G�l���M�[�������A���̃G�l���M�[�ɂ�蕨��B�������Ƃ����d�����������ƂɂȂ�܂��B���̂悤�ɁA�^�����Ă��镨��A�������ƂƂȂ����G�l���M�[���u�^���G�l���M�[�v�Ƃ����܂��B
���͊w�I�G�l���M�[
��L���ʒu�G�l���M�[���^���G�l���M�[�����킹�����̂��A�u�͊w�I�G�l���M�[�v�Ƃ����܂��B
�͊w�I�G�l���M�[���ʒu�G�l���M�[�{�^���G�l���M�[
�������G�l���M�[
���̂ɂ́A�͊w�I�G�l���M�[�̑��ɁA�����G�l���M�[�iU�j�������������݂��܂��B�����G�l���M�[�Ƃ́A���̂̒��̊e���q�ǂ��������݂��Ɉ������肠�����q�Ԉ��͂ɂ��ʒu�G�l���M�[�ƁA���q�⌴�q�������M�^���ɂ��^���G�l���M�[�ł��B
�������A��C�ɂ��ẮA�e���q�Ԃ̋������傫���̂ŁA���̕��q�ǂ����̈��͂��قƂ�Ǔ����Ȃ����߁A���q�Ԉ��͂ɂ��ʒu�G�l���M�[�͖����ł��܂��B
���Q�l�F���q�Ȃǂ��������U�����Ă����ԁ��M���傫���@�@���q�Ȃǂ����܂�U�����Ă��Ȃ���ԁ��M��������
���M�͊w�̑��@��
���炩���������G�l���M�[�uU�v�������C�́uA�v�ɁA�M�uQ�v���^����ꂽ�Ƃ���ƁA����ɂ��C�́uA�v���̐ς̖c���ŊO���ɁuW�v�����d�������āA���x�㏸�ɂ������G�l���M�[���uU�f�v�ɂȂ����Ƃ���ƁA���̊W�͎��̂悤�ɂȂ�܂��B
U�{Q��W�{U�f�@�����ό`����ƁA�@Q��W�{�iU�f-U�j�@�ƂȂ�A�����ŁA�iU�f-U�j�͓����G�l���M�[�̕ω���\���Ă����A��U�̋L���ɒu�������邱�Ƃ��ł��܂��B
����ɂ�鎮���AQ��W�{��U�@�ƂȂ�A�M�͊w�̑��@���ƌĂ����̂ɂȂ�܂��B�B
���̎��́u�C�̂ɔMQ����������ƁAW�����d�������āA�����G�l���M�[����U��������v�Ƃ������Ƃ�\���Ă��܂��B
�܂�A�C�̂��M�G�l���M�[Q����������ƁA�ꕔ�͖c���Ƃ����d�������邽�߂̊O���ւ��͊w�I�G�l���M�[W�ƂȂ�A�c��͉��x�㏸�ɂ�葝���������x�������G�l���M�[��U�Ƃ��Ē~������Ƃ������ƂɂȂ�܂��B���̓����G�l���M�[�́A�_�̂ł��郁�J�j�Y�����l�����ŏd�v�ȊT�O�ƂȂ�܂��B
�܂�A�M�͊w�̑��@���Ƃ́A�u�M�v�Ɓu�d���v�͓������̂ł���A�u�M����d���ցv�A�u�d������M�ցv�ϊ����邱�Ƃ��ł��A���̊Ԃɂ����Ă̓G�l���M�[���ۑ������Ƃ������Ƃ��`�������̂ł��B

��TOP
���f�M���k
�r�ɓ������C��A���s�X�g���ʼn����ē����̋�C�����k���܂��B���̎��A�u�C��A�̓s�X�g���ɂ��d�������ꂽ�v���ƂɂȂ�܂��B�s�X�g�����炳�ꂽ�d��W�̕����������G�l���M�[���������܂��B�����G�l���M�[����������ƁA�M�������Ă��Ȃ��̂ɋC��A�̉��x���㏸���܂��B������f�M���k�ɂ��f�M�����ƌ����܂��B
��قǂ̔M�͊w�̑��@���̎��ł́AQ�i�C��A�։�����ꂽ�M�ʁj��W�i�O���ɂ����d���j�{��U�i�~����ꂽ�����G�l���M�[�j�ł������A���̒f�M���k�ł͊O�������������u�M��Q�v�͂Ȃ��̂ŁA�O�����炳�ꂽ�u�d��W�v�̃G�l���M�[�̕����������G�l���M�[���������邱�ƂɂȂ�܂��B���������Ēf�M���k�ł͎��̎������藧���܂��B��U�i�����G�l���M�[�j���f�M���k�O�̓����G�l���M�[�{W�i�O�����炳�ꂽ�d���j
���f�M�c��
�r�ɋC��A����������ԂŃs�X�g���������܂��B���̎��s�X�g���͋C��A�ɉ����グ��ꂽ�悤�ɂ������܂��B�Ȃ̂ŁA������u�C��A���s�X�g���Ɏd���������v�Ƃ����A�d�����������A�����G�l���M�[������āA�C��A�̉��x��������܂��B������A�f�M�c���ɂ��f�M��p�Ƃ����܂��B
�����ł́A���̎������藧���܂��B��U�i�����G�l���M�[�j���f�M�c���O�̓����G�l���M�[�|W�i�O���ւ����d���j
����M�ƔM�e��
����M�Ƃ́A���͂܂��͑̐ψ��̏������ŁA�����Pg�i�Ώە��͈�̓_�j�̉��x���PK�i�P���r���j�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B��M�e���Ƃ������܂��B�������ώ��ł���Ε����̎��ʂɔ�Ⴗ�邽�߁A��M�͒P�ʎ��ʓ�����ƒ�߂��Ă��܂��B�P�ʂ��i/���E�j�i�W��-���p�[�O�����P���r���j�ŁA��M�̋L����c�i�X���[��c�j�ł��B
��M�̐��l�́A���ꂼ��̕����ɂ���ĈقȂ�܂��B�Ⴆ�A��M�������������͏��Ȃ��M�ʂʼn��x���ω����邽�߁A���܂�₷���A��߂₷�������������Ă��܂��B�t�ɁA��M���傫�������́A���x���グ�邽�߂ɑ����̔M�ʂ�K�v�Ƃ��A���܂�ɂ����A��߂ɂ��������������Ă��܂��B
��ȕ����Pg������̔�Mc�i�Q�l�l�j�@�P�ʂ͂i/���E�j
���� |
���x{�O��} |
��M |
�� |
�O |
�S�D�Q�P�V |
�� |
�Q�O |
�S�D�P�W�Q |
| �X | �|�P | �Q�D�P�O�O |
�C�� |
�R�D�X�S�O |
|
| ��C | �|�Q�O | �P�D�O�O�T |
| ��C | �O | �P�D�O�O�T |
��C |
�Q�O |
�P�D�O�O�U |
�S |
�O |
�O�D�S�R�T |
���M�e���Ƃ��A���͂܂��͑̐ψ��̏������ŁA�����i�Ώە��͓_�i�����j�̏W���́j�̉��x���PK�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B��M�ɕ��̂̎��ʂ��|�������̂ŁA�P�ʂ��i/�j�i�W��-���p�[�P���r���j�ŁA�M�e�ʂ̋L�����b�i���[�W�b�j�ł��B
���ɂ���Ɓ@C�������@�@�iC�F�M�e��J/K�@�@���F���ʂ��@�@���F��M�i/���E�j�j
����ϔ�M�ƒ舳��M����у}�C���[�̊W��
����ϔ�M�Ƃ́A�̐ρivolume�j���̏������ŁA�P�ʗʂP�s������̕����̉��x���PK�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B��e��M�Ƃ������܂��B�P�ʂ͂i/�j���E�j�i�W��-���p�[�L���O�����P���r���j�ŁA�L����Cv�ł��B
���舳��M�Ƃ́A���́ipressure�j���̏������ŁA�P�ʗʂP�s������̕����̉��x���PK�i���P���j�グ��̂ɕK�v�ȔM�ʂ̂��Ƃł��B�P�ʂ͂i/�j���E�j�i�W��-���p�[�L���O�����P���r���j�ŁA�L����Cp�ł��B
���}�C���[�̊W��
�舳��MCp�|��ϔ�MCv��R�i�C�̒萔�j
���z�C�̂ɂ����āA�舳��MCp�ƒ�ϔ�MCv�̍��͋C�̒萔R�ɓ������B
�����̓���
�P�@�ő̂̕X�́A�t�̂̐����̐ς��傫���y���B
�Q�@���̉t�̂ɔ�ׂāA�Z�_�ƕ��_�������B
�R�@���q���m�����т���͂������̂ŁA�\�ʒ��͂��傫���B
�S�@��M���傫���̂ŁA�R�ĕ����̍��M���ɐ����|����ƁA�������㏸���ĕ�������܂łɂ��̔R�ĕ��������R�̔M��D���B�B
�T�@�����M�i�C���M�j���傫���̂ŁA�����C�́i�����C�j�ɂȂ�Ƃ��Ɏ��͂��瑽���̔M��D���B
�U�@�M�`�����������B
�V�@�l�X�ȕ�����n�����B
��TOP
���C���X�x��
���������̊Ԃɂ����C��ɓ������C���̍�����C��́A�C���̒Ⴂ��C��̕��ֈړ����悤�Ƃ��܂��B���̗͂��C���X�x�͂Ƃ����܂��B�C���̍����傫���قǁA���̋C���X�x�͂͑傫���Ȃ�A��C�Ɉړ���������͂ƂȂ��ĕ��������܂��B

��TOP
���C���X�x�͂Ɛ×͊w���t
�����������ɓ����C���X�x�͂Ɛ×͊w���t
��TOP
���R���I������
�n���̎��]�́A�k�ɓ_�ォ�猩��Ɣ����v���A��ɓ_�ォ�猩��Ǝ��v���ɉ�]���Ă��܂��B
���������āA�k�����ɂ����āA�k�シ�镨�̂͏��X�ɓ����ɐi�ނ悤�Ɍ����A�쉺���镨�̂͏��X�ɐ����ɐi�ނ悤�Ɍ����܂��B���́u�������̗́v���R���I���̗͂Ƃ����܂��B
�R���I���̗͂́A������ς���͂͂���܂����A������ς���͂͂���܂���B
���ɁA�R���I���̗͂̑傫���ɂ��čl���܂��B
�R���I���̗͂́A�ԓ��ł͂O�i�[���j�ł����A���ܓx�قǑ傫���Ȃ�A�k�ɂƓ�ɂł͍ő�ƂȂ�܂��B
����ɁA�R���I���̗͂��傫���Ȃ�v�f�Ƃ��ẮA���ܓx�̂ق��A���ʂ��傫���A���̂̑��x�������A�قǑ傫���Ȃ�܂��B
�R���I���̗͂̑傫�������ɂ���Ǝ��̂悤�ɂȂ�܂��B
���R���I���̗́�
F�����~�Q��Vsin���i�Q�I���K�@���C�@�T�C���@�t�@�C�j�@
�e�F�R���I���̗́@�@
���F���ʁi�����j�@�@
���F�n���̊p���x�i
V�F���̂̑��x�i
���F�ܓx
���R���I���p�����[�^��
��L�@�̎��̂����A����m�ƕ��̂̑��xV�ȊO�̐��l�͈ܓx�ɂ���Č��܂���̂Ȃ̂ŁA����m�ƕ��̂̑��xV���u�P�v�Ƃ��Ď��̎��ɂȂ�܂��B������A�R���I���p�����[�^�Ƃ����܂��B
�����Q��sin���@�i�R���I�����q�܂��͘f���ߓx�Ƃ������܂��j�A
���F�n���̊p���x
���F�R���I���������ꏊ�̈ܓx
���@�̎��̂����A���ʂƕ��̂̑��x�ȊO�̒l�͈ܓx�ɂ���Č��܂�̂ŁA���̎����R���I���p�����[�^�Ƃ���B
���@�̎����A�̎���������Ɓ�
F=mVf�@�B�@
���̎����C�ی��ۂɓ��Ă͂߂��ꍇ�̊e�v�f��
m�F��C��̎���
V�F����
���F���]�̊p���x�̒l�i�V�D�Q�X�Q�~
���F�R���I���p�����[�^
�ƂȂ�܂��B
���@���B�̎��̎��ʂ����P�����Ƃ����P�ʎ��ʂ�p����ƁA�@���B�̎��͂��ꂼ�ꎟ�̂悤�ɂȂ�܂���
F���Q��Vsin���@�@�f
F=Vf�@�B�f
���ꂪ�A�P�ʎ��ʂP�s�̋�C��ɓ����R���I���̗͂̑傫���ɂȂ�܂��B�P�ʂ�
�����ŁAF=mVf��F�����~�Q��Vsin���̎�����A�R���I���̗�F�Ǝ��ʂ��E�R���I���̗�F�ƕ��̂̑��x�u�E�R���I���̗�F�ƃR���I���p�����[�^���E�R���I���̗�F��sin���i�R���I���p�����[�^�ɂ��Q���̒l�i�V�D�Q�X�Q�~
���������̏ꍇ�̃R���I���̗͈͂ܓx�Ō��܂�B
�ܓx�����̏ꍇ�̃R���I���̗͕͂����Ō��܂�B
�ƂȂ�܂��B
�Q�l�܂ŁA�ܓx���Ƃ̃R���I���̗͂̑傫�����v�Z���Ă݂܂��B
F���Q��Vsin���@���̎������Ɉܓx�̐��l�Ă͂߂܂��B
���ܓx�����k�܂O�x�i�ԓ���j
F���Q��Vsin�O���@sin0�����O
F���Q��V�~�O�@
F���O�i�[���j
�ԓ���ł̓R���I���̗͓͂����Ȃ��B
���ܓx�����k�܂R�O�x
F���Q��Vsin�R�O���@sin�R�O�����O�D�T
F���Q��V�~�P�@
F����V
���ܓx�����k�܂X�O�x�i�k�Ɂj
F���Q��Vsin�X�O���@sin�X�O�����P
F���Q��V�~�P�@
F���Q��V
�k�ɂƓ�ɂł̓R���I���̗͍͂ő�ƂȂ�B
��TOP
���n�t��(�������ӂ��j
�n�t���Ƃ́A�C���X�x�͂ƃR���I�������̉e�����A���̑o�����ނ荇�������ʐ����镗�ł��B�Î~���Ă����C��ɂ͋C���X�x�͂��͂��炢�āA���C���������C�����Ɍ������ĕ��ƂȂ��ē����n�߂܂��B
���̑��xV�����������ƁA���̕����ɔ�Ⴕ�ăR���I���������傫���Ȃ�܂��iF���Q��Vsin���j�B�k�����Ŗk�シ�镗�́A�R���I���̗͂��傫���Ȃ�قǂɁA�E���i�����j�ւƋȂ�����悤�ɂȂ�܂��B�ŏI�I�ɂ́A�C���X�x�͂ƃR���I���̗͂��o�����X��ۂ��āA�������ɉ����ĕ��������悤�ɂȂ�܂��B���ꂪ�n�t���ł��B�n�t���ɂȂ�ƁA�����͂���ȏ��������邱�Ƃ��Ȃ��A�܂��������ς��Ȃ����肵�����ƂȂ�܂��B
�k�����Ŕ�������n�t���́A��C�����i�ፂ�x���j������Ɍ���悤�ɂ��Đ����܂��B�씼���ł͋t�ɁA��C�������E��Ɍ���悤�ɂ��Đ����܂��B
�Ȃ��A�C���X�x�͂ƃR���I���̗͂��ނ荇������Ԃ��n�t�����t�Ƃ����܂��B

���n�t���̕��������߂�
�n�t���́A�C���X�x�͂ƃR���I���̗͂��o�����X�i�C���X�x�́��R���I���̗́j���Ƃ��Ă���̂ŁA���̎��ɂ��n�t���̕��������߂邱�Ƃ��ł��܂��B

��TOP
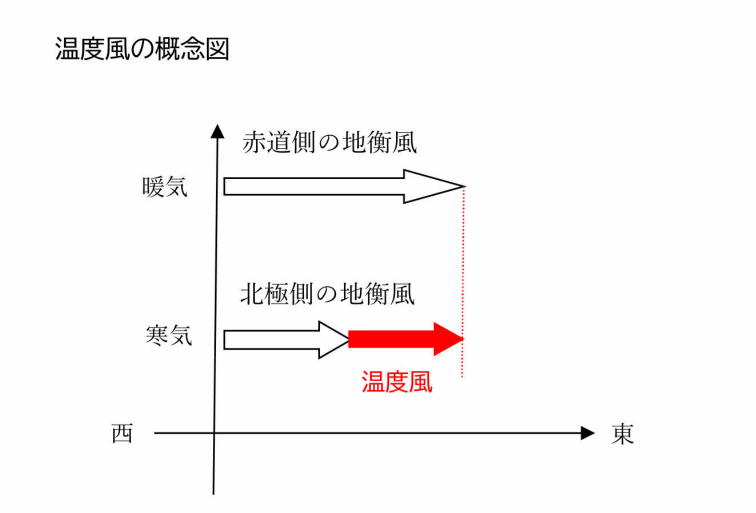
�����x���i����ǂӂ��j
�n�t���̉��������̕����E�����̍������x���Ƃ����܂��B���x���͎��ۂɐ����Ă��镗�ł͂Ȃ��A�Q�n�_�̕��x�N�g���̍��������܂��B
�n���̑�C�́A�ԓ��t�߂ł͒g�����A�k�ɕt�߂ł͗₽���B
�ԓ����̒g������C��͖c������̂ŁA���̓����ʂ́A���x�̍������Ɉʒu����B
�t�ɁA�k�ɑ��̗₽����C��͈��k����̂ŁA���̓����ʂ́A���x�̒Ⴂ���Ɉʒu����B
���������āA���̒g�C�Ɗ��C�̊Ԃɂ��C���X�x���������āA�n�t������������B
�C���X�x�͂͏��قǑ傫���Ȃ邽�߁A�n�t�������قǑ傫���Ȃ�A�n��ɋ߂��قǒn�t���͏������Ȃ�B
���̎��̕����̍��i�Q�n�_�̕��x�N�g���̍��j�����x���Ƃ����B
�k�����ł̒n�t���́A�E����g������C�i�ԓ����j�A������₽����C�i�k�ɑ��j�Ƃ��鐼���ƂȂ��Ă��邽�߁A���x�����g������C���E���ɂ��Đ����ƂȂ��Ă���B


��TOP