あした天気になあれ!
温位
■温位
■温位の保存
■相当温位と湿舌
■温位(potential temperature)
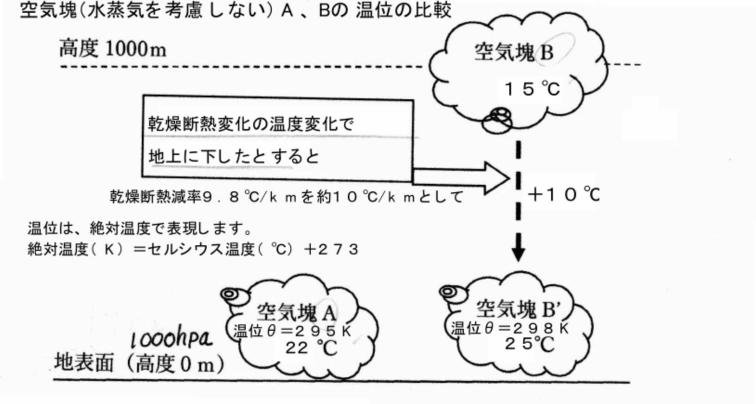
地上0mで1000hPaの地点には温度22℃の空気塊(水蒸気を考慮しない)A、高度1000mの上空には温度15℃の空気塊(水蒸気を考慮しない)Bがあるとします。
単に温度の比較では、空気塊Aの方が空気塊Bより7℃暖かいことになりますが、ことなる高度(気圧)に位置する空気塊の寒暖を比較することは妥当ではありません。
そこで、空気塊Bを空気塊Aの気圧と同じ1000hPanの条件下に揃えて比較することにします。この場合、高度1000mにある空気塊Bを乾燥断熱変化(熱の出入りのない、水蒸気の凝結もない状態)により高度0m(1000hPa)に下します。
乾燥断熱減率(9.8℃/km)を約10℃/kmとすると、高度0mで気圧1000hPaに下した空気塊Bの温度はプラス10℃となり、その温度は空気塊B’として25℃となります。この空気塊B’の温度25℃が温位θ298Kとなります。
温位の単位は絶対温度(K)で表し、温位記号はθ(シーター)を用います。
このように、温位とは「空気塊(水蒸気を考慮しない)を乾燥断熱変化により1000hPaの高度に移動させた時の温度」と定義されています。
高度(気圧)の相違する複数の空気塊の寒暖を比較する場合には、それぞれの空気塊の温位を算出して比べることとなります。
なお、理想気体の状態方程式によると、同じ圧力場における気体の密度は温度に反比例するため、単位面積(g/cm3=(質量)g÷(体積)cm3)あたりで比較すると、温位の高い気体は密度が小さくなるので軽く、温位の低い気体は密度が大きくなるので重い。
以上により、温位は未飽和の空気塊による大気の安定か不安定かの状態を考えるときに役立ちます。
例として、地上A地点の気圧を1000hPaとして気温が15℃の空気塊があるとします。
そして、そのA地点の上空1000mに気温8℃の空気塊Bがあるとします。ただし、何れの空気塊も水蒸気を考慮しません。
この場合の気温だけで比較すると、上空が冷たいのでその空気塊Bは下降してくるように見えますが、現状は空気塊Bの下降はなく大気の成層は安定しています。そこで、両者の温位を考えます。空気塊Aの温位θは288K(気温15℃+273)です。空気塊Bの温位θは291K(気温8℃+断熱変化10℃+273)となり、空気塊Bの温位が3K高いことが分かります。なので空気塊Bの気体の密度が小さく軽いため下降しないことが分かります。このように温位は大気の状態を考えるときに役立ちます。
■温位の保存
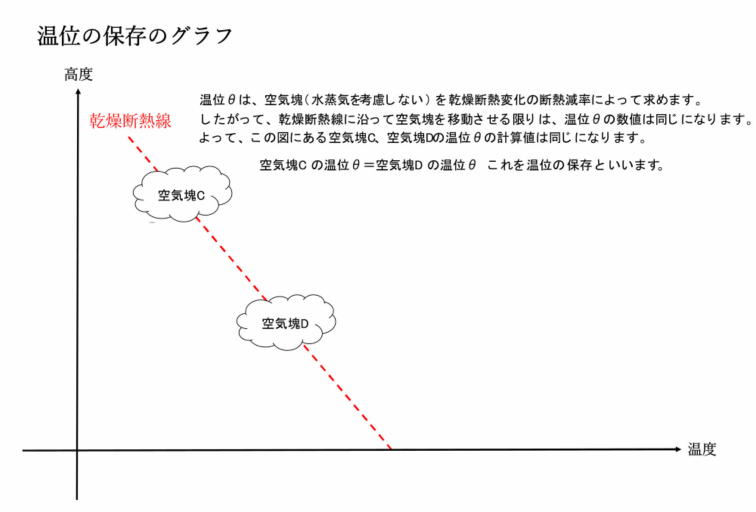
温位θは、空気塊(水蒸気を考慮しない)を乾燥断熱変化させて数値を求めるものなので、乾燥断熱線(空気塊の断熱減率(乾燥断熱減率)を表したグラフ線)に沿って変化している限り、それぞれの温位θに変化はありません。したがって、同じ乾燥断熱線上にある複数の空気塊の温位は、すべて同じになります。これを温位の保存といいます。
温位θは、水蒸気を考慮しない空気塊を乾燥断熱変化させてその数値を求めましたが、相当温位は、水蒸気を考慮した空気塊で考えます。水蒸気を含む湿潤空気塊が断熱変化によりその水蒸気のすべてが凝結することによって放出される凝結熱(潜熱)分の温度をプラスした値が相当温位θeです。したがって、未飽和ではあっても水蒸気を含む空気塊の本当の状態を知ることができます。この相当温位は、乾燥断熱変化でも湿潤断熱変化でも値が変わらなく保存されます。なぜかというと、相当温位は「凝結熱で温まった空気塊の温位」と考えるため、空気塊の水蒸気量がゼロだと、凝結熱が発生しないので凝結熱もゼロとなり「温位θ=相当温位θe」となるからです。したがって、空気塊の水蒸気量が多いほど相当温位θeは温位θよりも高くなります。さらに、気温が高いほど相当温位の値は大きくなり、逆に気温が低いと相当温位の値は小さくなります。したがって、相当温位を確認することで、空気がどれだけ暖かく湿っているかを数値で確認することができます。
相当温位が大きい空気ほど高温多湿、相当温位が小さい空気ほど低温乾燥ということが分かります。
この高温多湿の空気が入り込むと大雨が降りやすくなります。相当温位が大きい場所として、夏季は336K以上、冬季は324K以上を高相当温位域(高θe域)といい、天気予報では大雨の目安とします。
日本付近の南側から高温多湿の空気が「舌」のような形で入り込むことがあり、これを「湿舌」といいます。この湿舌が入り込むと南側からどんどん高温多湿の空気が流れ込み、記録的な大雨となることがあります。この大雨を予想するため、日本付近の相当温位の分布を表した天気図FXJP854があります。
このように相当温位は大気の不安定度を考えるときに大いに役に立ちます。
※参考:温位θと相当温位θeの間には、θe=θ+2.8wの近似値が成り立ちます。wは混合比です。
↑TOP
■温位の保存
■相当温位と湿舌
■温位(potential temperature)

地上0mで1000hPaの地点には温度22℃の空気塊(水蒸気を考慮しない)A、高度1000mの上空には温度15℃の空気塊(水蒸気を考慮しない)Bがあるとします。
単に温度の比較では、空気塊Aの方が空気塊Bより7℃暖かいことになりますが、ことなる高度(気圧)に位置する空気塊の寒暖を比較することは妥当ではありません。
そこで、空気塊Bを空気塊Aの気圧と同じ1000hPanの条件下に揃えて比較することにします。この場合、高度1000mにある空気塊Bを乾燥断熱変化(熱の出入りのない、水蒸気の凝結もない状態)により高度0m(1000hPa)に下します。
乾燥断熱減率(9.8℃/km)を約10℃/kmとすると、高度0mで気圧1000hPaに下した空気塊Bの温度はプラス10℃となり、その温度は空気塊B’として25℃となります。この空気塊B’の温度25℃が温位θ298Kとなります。
温位の単位は絶対温度(K)で表し、温位記号はθ(シーター)を用います。
このように、温位とは「空気塊(水蒸気を考慮しない)を乾燥断熱変化により1000hPaの高度に移動させた時の温度」と定義されています。
高度(気圧)の相違する複数の空気塊の寒暖を比較する場合には、それぞれの空気塊の温位を算出して比べることとなります。
なお、理想気体の状態方程式によると、同じ圧力場における気体の密度は温度に反比例するため、単位面積(g/cm3=(質量)g÷(体積)cm3)あたりで比較すると、温位の高い気体は密度が小さくなるので軽く、温位の低い気体は密度が大きくなるので重い。
以上により、温位は未飽和の空気塊による大気の安定か不安定かの状態を考えるときに役立ちます。
例として、地上A地点の気圧を1000hPaとして気温が15℃の空気塊があるとします。
そして、そのA地点の上空1000mに気温8℃の空気塊Bがあるとします。ただし、何れの空気塊も水蒸気を考慮しません。
この場合の気温だけで比較すると、上空が冷たいのでその空気塊Bは下降してくるように見えますが、現状は空気塊Bの下降はなく大気の成層は安定しています。そこで、両者の温位を考えます。空気塊Aの温位θは288K(気温15℃+273)です。空気塊Bの温位θは291K(気温8℃+断熱変化10℃+273)となり、空気塊Bの温位が3K高いことが分かります。なので空気塊Bの気体の密度が小さく軽いため下降しないことが分かります。このように温位は大気の状態を考えるときに役立ちます。
■温位の保存
温位θは、空気塊(水蒸気を考慮しない)を乾燥断熱変化させて数値を求めるものなので、乾燥断熱線(空気塊の断熱減率(乾燥断熱減率)を表したグラフ線)に沿って変化している限り、それぞれの温位θに変化はありません。したがって、同じ乾燥断熱線上にある複数の空気塊の温位は、すべて同じになります。これを温位の保存といいます。

■相当温位と湿舌
温位θは、水蒸気を考慮しない空気塊を乾燥断熱変化させてその数値を求めましたが、相当温位は、水蒸気を考慮した空気塊で考えます。水蒸気を含む湿潤空気塊が断熱変化によりその水蒸気のすべてが凝結することによって放出される凝結熱(潜熱)分の温度をプラスした値が相当温位θeです。したがって、未飽和ではあっても水蒸気を含む空気塊の本当の状態を知ることができます。この相当温位は、乾燥断熱変化でも湿潤断熱変化でも値が変わらなく保存されます。なぜかというと、相当温位は「凝結熱で温まった空気塊の温位」と考えるため、空気塊の水蒸気量がゼロだと、凝結熱が発生しないので凝結熱もゼロとなり「温位θ=相当温位θe」となるからです。したがって、空気塊の水蒸気量が多いほど相当温位θeは温位θよりも高くなります。さらに、気温が高いほど相当温位の値は大きくなり、逆に気温が低いと相当温位の値は小さくなります。したがって、相当温位を確認することで、空気がどれだけ暖かく湿っているかを数値で確認することができます。
相当温位が大きい空気ほど高温多湿、相当温位が小さい空気ほど低温乾燥ということが分かります。
この高温多湿の空気が入り込むと大雨が降りやすくなります。相当温位が大きい場所として、夏季は336K以上、冬季は324K以上を高相当温位域(高θe域)といい、天気予報では大雨の目安とします。
日本付近の南側から高温多湿の空気が「舌」のような形で入り込むことがあり、これを「湿舌」といいます。この湿舌が入り込むと南側からどんどん高温多湿の空気が流れ込み、記録的な大雨となることがあります。この大雨を予想するため、日本付近の相当温位の分布を表した天気図FXJP854があります。
このように相当温位は大気の不安定度を考えるときに大いに役に立ちます。
※参考:温位θと相当温位θeの間には、θe=θ+2.8wの近似値が成り立ちます。wは混合比です。
↑TOP